Draw Circle Equations Online Test

Equation of a Circle Reckoner

Created past Bogna Szyk and Hanna Pamuła , PhD candidate

Concluding updated:

Mar 25, 2022

Table of contents:

• What is a standard equation of a circle?
• Parametric equation of a circumvolve
• Standard equation to parametric equation of the circle
• How to find the equation of a circumvolve?
• Some other grade of the circle equation
• How to utilize this equation of a circle calculator?

No thing your proficiency in the geometry of a circle, the equation of the circle may notwithstanding make your caput spin. If this is the case, don't worry! This standard equation of a circumvolve calculator will assistance you determine the radius and the center coordinates of a circumvolve in a blink of an eye. If you are curious almost how to notice the equation of a circle, scroll downwards, and you'll find an explanation of the formula.

If the geometric shape you're trying to analyze looks a bit squashed, it's probably an ellipse. In such a instance, head straight to our ellipse calculator!

🔎 If you're new to circles, maybe other more than basic tools tin be helpful to you, such as circumference and area of a circle, circumference to diameter, or square footage of a circle, and circle length calculators.

What is a standard equation of a circle?

The standard equation of a circle is a style to depict all points lying on a circle with merely one formula:

(x - A)² + (y - B)² = r²

(x, y) are the coordinates of any point lying on the circumference of the circle. It ways that as long as y'all know all of the constants, you tin input any ten value to figure out the coordinates of any arbitrary point on the circle.

(A, B) are the coordinates of the centre point. Merely careful almost the + and - signs here; for example, a circle with an equation of the form (x - 3)² + (y + 3)² = 5² will have a center point at (iii, -iii).

r² is the radius of the circle, raised to the power of two. To discover the radius, simply take a square root of this value.

Our equation of the circle estimator finds not merely these values, but also the diameter, circumference and expanse of the circumvolve - all to save you time!

Parametric equation of a circle

Equation of a circle may be defined in different ways; non merely in the standard form shown to a higher place. A circle can besides be described every bit the locus of all the points that satisfy the equations:

x = r * cos(α)

y = r * sin(α)

where

(10, y) are the coordinates of whatever betoken on the circle, as before;

r is the radius of the circumvolve, and

α is the parameter - the bending subtended by the point at the circle'due south center.

If you shift the center of the circle to (A, B) coordinates, you'll simply add them to the x and y coordinates to go the general parametric equation of a circumvolve:

x = A + r * cos(α)

y = B + r * sin(α)

Every bit in a higher place, you should be conscientious almost the signs of the center indicate.

Standard equation to parametric equation of the circle

To demonstrate that these 2 forms of the circle formula are equivalent, allow's do a conversion betwixt them:

1. Starting from the parametric equation, we know that

x = r * cos(t) so cos(t) = x / r

y = r * sin(t) so sin(t) = y / r

2. Let's take the well-known Pythagorean trigonometric identity:

sin²(t) + cos²(t) = one

3. Combine the identity with the parametric equations:

(y / r)² + (10 / r)² = i

4. Then remove the parentheses:

y² / r² + x² / r² = 1

5. And finally, multiply by r² (letting r = 1) and put the elements in the right order

ten² + y² = 1

Here we are! That's the standard equation of a circle.

How to find the equation of a circle?

OK, y'all've learned virtually unlike circle equations. Only where are they come from? Let'south find out!

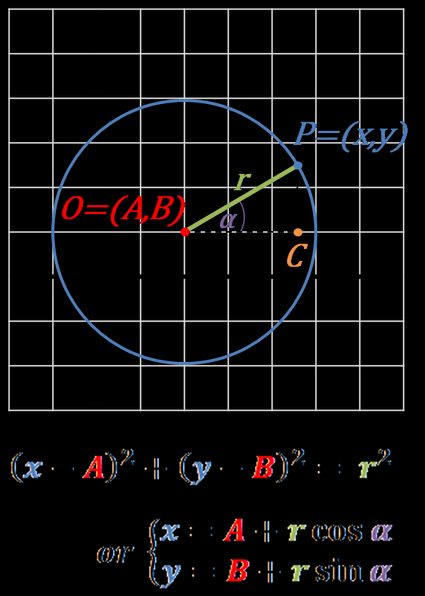
1. Cull the center O = (A, B) of your circumvolve. Don't choose it equally the origin of the coordinate arrangement.
2. Draw a circle with a chosen radius r.
3. Pick whatsoever betoken on the circle. Assume the coordinates of that point are P = (10,y).
4. The angle POC is equal to α.

Nifty, we have all the data needed. Now we just need to employ one geometric law or basic piece of trigonometry to tie the given values together:

• Use the distance formula:

  √[(x₂ - x₁)² + (y₂ - y₁)²] = r so

  √[(x - A)² + (y - B)²] = r and foursquare the obtained formula to get the standard equation of a circumvolve:

  (10 - A)² + (y - B)² = r²

• Use the Pythagorean theorem:

  r is a hypotenuse of a correct triangle POC, so from Pythagorean theorem nosotros can write:

  |OC|² + |CP|² = r²

  As well we know that:

  |OC| = |x - A|

  |CP| = |y - B|

  Coming back to the commencement equation nosotros get:

  |x - A|² + |y - B|² = r² equally a² = (−a)², the above equation works for every quadrant, not only the first 1. Then the equation can be simplified to a standard formula:

  (x - A)² + (y - B)² = r²

• Use trigonometry:

  express the POC triangle sides using sine and cosine functions:

  cos(α) = OC / r so OC = r * cos(α)

  sin(α) = CP / r so CP = r * sin(α)

  Coordinates of betoken P may be expressed as:

  x = A + OC and y = B + CP, and so

  x = A + r * cos(α)

  y = B + r * sin(α)

  Two last equations represent the parametric equations of the circumvolve.

Now equally y'all know how to notice the equation of a circle, give this estimator a attempt!

Some other form of the circumvolve equation

Quite often, you will come beyond another form of the circumvolve equation. It looks like this:

x² + y² + Dx + Ey + F = 0

This is the full general form of a circle equation - the same as the standard form, but expanded. It is possible to get to the standard form from hither with but a few simple operations - all you take to practise is follow the steps below!

1. Offset with your general equation, for case:

x² + y² + 4x - 6y + 8 = 0

2. Put the x's and y'due south together:

(x² + 4x) + (y² - 6y) + 8 = 0

3. Move the constant to the right hand side of the equation:

(x² + 4x) + (y² - 6y) = -8

4. Now, complete the square for 10. In order to do it, you need to take half of the 4, square it, and add to both sides:

(x² + 4x + 4) + (y² - 6y) = -viii + 4

5. Repeat the previous footstep, this time completing the square for y:

(x² + 4x + 4) + (y² - 6y + ix) = -8 + 4 + 9

6. Simplify the x- and y-terms according to the factoring formulas:

(x + two)² + (y - 3)² = 5

You're washed - this is the standard course of a circle with a middle at (-two, 3) and a radius equal to √5.

Naturally, you don't have to get through this whole process by yourself. Use this equation of a circle calculator instead!

How to use this equation of a circumvolve calculator?

If you are still unsure how to use our tool, have a expect at this simple instance beneath.

1. Assume you lot want to apply the standard equation of a circle. So it's the beginning part of the calculator.
2. Type the given data. Let's say that your equation of a circle parameters are equal to A = seven, B = -ii and C = 9.
3. Tadaa! The equation of a circle calculator did the chore! The tool will shows you what the parameters are in the other forms of an equation, explaining what the A and B values are (the circle center coordinates), and it volition additionally calculates other values such as:

• radius - which is equal to three for our circumvolve,
• bore - half-dozen in our case,
• area is 28.3 for our instance, and
• circumference of the circle is equal to 18.85.

In this calculator, nosotros didn't put any units, as in many cases you don't need them, because you lot're working with the coordinates. If yous need some units - like, e.g. inches, feet, or centimeters - just add them to the obtained results. Don't forget that the circles surface area will have squared units of length!

Try our equation of a sphere reckoner to do the same thing, only with spheres!

Bogna Szyk and Hanna Pamuła , PhD candidate

x = A + r cos(α), y = B + r sin(α)

x² + y² + Dx + Ey + F = 0

Arc length Area of a circle Circumvolve calc: find c, d, a, r … 5 more

nunnallashom.blogspot.com

Source: https://www.omnicalculator.com/math/circle-equation

Share this post